Bodový součin vektorů v souřadnicích v prostoru. Bodový součin vektorů: vlastnosti, příklady výpočtů, fyzikální význam

Křížový součin a bodový součin usnadňují výpočet úhlu mezi vektory. Nechť jsou dány dva vektory $\overline(a)$ a $\overline(b)$, orientovaný úhel mezi nimi je roven $\varphi$. Vypočítejme hodnoty $x = (\overline(a),\overline(b))$ a $y = [\overline(a),\overline(b)]$. Potom $x=r\cos\varphi$, $y=r\sin\varphi$, kde $r=|\overline(a)|\cdot|\overline(b)|$, a $\varphi$ je požadovaný úhel, to znamená, že bod $(x, y)$ má polární úhel rovný $\varphi$, a proto $\varphi$ lze nalézt jako atan2(y, x).

Oblast trojúhelníku

Protože křížový součin obsahuje součin dvou vektorových délek a kosinus úhlu mezi nimi, lze křížový součin použít k výpočtu plochy trojúhelníku ABC:

$ S_(ABC) = \frac(1)(2)|[\overline(AB),\overline(AC)]| $.

Příslušnost bodu k přímce

Nechť je dán bod $P$ a přímka $AB$ (daná dvěma body $A$ a $B$). Je nutné zkontrolovat, zda bod patří k přímce $AB$.

Bod patří k přímce $AB$ právě tehdy, když jsou vektory $AP$ a $AB$ kolineární, tj. když $ [ \overline(AP), \overline(AB)]=0 $.

Příslušnost bodu k paprsku

Nechť je dán bod $P$ a paprsek $AB$ (definovaný dvěma body - počátek paprsku $A$ a bod na paprsku $B$). Je nutné zkontrolovat, zda bod patří paprsku $AB$.

K podmínce, že bod $P$ patří přímce $AB$, je nutné přidat další podmínku - vektory $AP$ a $AB$ jsou kosměrné, to znamená, že jsou kolineární a jejich skalární součin je nezáporné, tedy $(\overline(AB), \overline(AP ))\ge 0$.

Příslušnost bodu k segmentu

Nechť je dán bod $P$ a segment $AB$. Je nutné zkontrolovat, zda bod patří do segmentu $AB$.

V tomto případě musí bod patřit jak paprsku $AB$, tak paprsku $BA$, takže je třeba zkontrolovat následující podmínky:

$[\overline(AP), \overline(AB)]=0$,

$(\overline(AB), \overline(AP))\ge 0$,

$(\overline(BA), \overline(BP))\ge 0$.

Vzdálenost od bodu k řádku

Nechť je dán bod $P$ a přímka $AB$ (daná dvěma body $A$ a $B$). Je nutné zjistit vzdálenost od bodu úsečky $AB$.

Uvažujme trojúhelník ABP. Na jedné straně je jeho plocha rovna $S_(ABP)=\frac(1)(2)|[\overline(AB),\overline(AP) ]|$.

Na druhou stranu, jeho plocha je rovna $S_(ABP)= \frac(1)(2)h |AB|$, kde $h$ je výška upuštěná od bodu $P$, tedy vzdálenost od $P$ do $ AB$. Kde $h=|[\overline(AB),\overline(AP)]|/|AB|$.

Vzdálenost od bodu k paprsku

Nechť je dán bod $P$ a paprsek $AB$ (definovaný dvěma body - počátek paprsku $A$ a bod na paprsku $B$). Je nutné zjistit vzdálenost bodu k paprsku, to znamená délku nejkratšího úseku od bodu $P$ k libovolnému bodu na paprsku.

Tato vzdálenost se rovná buď délce $AP$ nebo vzdálenosti od bodu $P$ k přímce $AB$. Který z případů nastane, lze snadno určit podle vzájemné polohy paprsku a bodu. Pokud je úhel PAB ostrý, tedy $(\overline(AB),\overline(AP)) > 0$, pak bude odpovědí vzdálenost od bodu $P$ k přímce $AB$, jinak odpovědí bude délka segmentu $AB$.

Vzdálenost od bodu k segmentu

Nechť je dán bod $P$ a segment $AB$. Je nutné zjistit vzdálenost od $P$ k segmentu $AB$.

Pokud základna kolmice pokleslá z $P$ na přímku $AB$ připadá na segment $AB$, což lze ověřit podmínkami

$(\overline(AP), \overline(AB))\ge 0$,

$(\overline(BP), \overline(BA))\ge 0$,

pak bude odpovědí vzdálenost od bodu $P$ k přímce $AB$. Jinak bude vzdálenost rovna $\min(AP, BP)$.

Bodový součin vektorů

Nadále se zabýváme vektory. Na první lekci Vektory pro figuríny Podívali jsme se na koncept vektoru, akce s vektory, vektorové souřadnice a nejjednodušší problémy s vektory. Pokud jste se na tuto stránku dostali poprvé z vyhledávače, důrazně doporučuji přečíst si výše uvedený úvodní článek, protože pro zvládnutí látky je třeba znát termíny a zápisy, které používám, mít základní znalosti o vektorech a umět řešit základní problémy. Tato lekce je logickým pokračováním tématu a podrobně v ní rozeberu typické úlohy, které využívají skalární součin vektorů. Toto je VELMI DŮLEŽITÁ aktivita.. Pokuste se nepřeskakovat příklady, přicházejí s užitečným bonusem – cvičení vám pomůže upevnit probraný materiál a zlepšit se v řešení běžných problémů v analytické geometrii.

Sčítání vektorů, násobení vektoru číslem.... Bylo by naivní si myslet, že matematici nepřišli na něco jiného. Kromě již diskutovaných akcí existuje řada dalších operací s vektory, jmenovitě: bodový součin vektorů, vektorový součin vektorů A smíšený součin vektorů. Skalární součin vektorů je nám známý ze školy, zbylé dva součiny tradičně patří do kurzu vyšší matematiky. Témata jsou jednoduchá, algoritmus pro řešení mnoha problémů přímočarý a srozumitelný. Jediná věc. Informací je slušné množství, a tak je nežádoucí snažit se zvládnout a řešit VŠE NARAZ. To platí zejména pro figuríny, věřte, že autor si absolutně nechce připadat jako Chikatilo z matematiky. No, z matematiky samozřejmě taky ne =) Připravenější studenti mohou používat materiály selektivně, v určitém smyslu „získat“ chybějící znalosti, pro vás budu neškodný hrabě Drákula =)

Pojďme konečně otevřít dveře a s nadšením sledovat, co se stane, když se dva vektory setkají...

Definice skalárního součinu vektorů.
Vlastnosti skalárního součinu. Typické úkoly

Koncept bodového produktu

Nejprve o úhel mezi vektory. Myslím, že každý intuitivně chápe, jaký je úhel mezi vektory, ale pro každý případ trochu podrobněji. Uvažujme volné nenulové vektory a . Pokud tyto vektory vynesete z libovolného bodu, získáte obrázek, který si již mnozí v duchu představili:

Přiznám se, zde jsem popsal situaci pouze v rovině porozumění. Pokud potřebujete přesnou definici úhlu mezi vektory, podívejte se prosím do učebnice, pro praktické problémy ji v zásadě nepotřebujeme. Také ZDE A ZDE budu místy ignorovat nulové vektory pro jejich malý praktický význam. Udělal jsem rezervaci speciálně pro pokročilé návštěvníky stránek, kteří mi mohou vyčítat teoretickou neúplnost některých následných tvrzení.

V literatuře se symbol úhlu často přeskakuje a jednoduše se píše.

Definice: Skalární součin dvou vektorů je ČÍSLO rovné součinu délek těchto vektorů a kosinu úhlu mezi nimi:

Nyní je to docela přísná definice.

Zaměřujeme se na základní informace:

Označení: skalární součin je označen nebo jednoduše.

Výsledkem operace je ČÍSLO: Vektor se vynásobí vektorem a výsledkem je číslo. Pokud jsou délky vektorů čísla, kosinus úhlu je číslo, pak jejich součin bude také číslo.

Jen pár příkladů zahřívání:

Příklad 1

Řešení: Používáme vzorec . V tomto případě:

Odpovědět:

Hodnoty kosinu lze nalézt v trigonometrická tabulka. Doporučuji vytisknout - bude potřeba téměř ve všech úsecích věže a bude potřeba mnohokrát.

Z čistě matematického hlediska je skalární součin bezrozměrný, to znamená, že výsledek je v tomto případě jen číslo a je to. Z hlediska fyzikálních problémů má skalární součin vždy určitý fyzikální význam, to znamená, že po výsledku musí být označena ta či ona fyzikální jednotka. Kanonický příklad výpočtu práce síly lze nalézt v jakékoli učebnici (vzorec je přesně skalárním součinem). Práce síly se měří v joulech, proto bude odpověď napsána zcela konkrétně, například .

Příklad 2

Najdi jestli a úhel mezi vektory je roven .

Toto je příklad, který můžete vyřešit sami, odpověď je na konci lekce.

Úhel mezi vektory a hodnotou bodového součinu

V příkladu 1 se skalární součin ukázal jako pozitivní a v příkladu 2 se ukázal jako negativní. Pojďme zjistit, na čem závisí znaménko skalárního součinu. Podívejme se na náš vzorec: . Délky nenulových vektorů jsou vždy kladné: , takže znaménko může záviset pouze na hodnotě kosinusu.

Poznámka: Pro lepší pochopení níže uvedených informací je lepší si prostudovat kosinusový graf v návodu Funkční grafy a vlastnosti. Podívejte se, jak se kosinus chová na segmentu.

Jak již bylo uvedeno, úhel mezi vektory se může uvnitř měnit a jsou možné následující případy:

1) Pokud roh mezi vektory pikantní: (od 0 do 90 stupňů), pak , A bodový součin bude pozitivní spolurežírovaný, pak je úhel mezi nimi považován za nulový a skalární součin bude také kladný. Vzhledem k tomu, vzorec zjednodušuje: .

2) Pokud roh mezi vektory otupit: (od 90 do 180 stupňů), pak a odpovídajícím způsobem, dot product je negativní: . Zvláštní případ: pokud vektory opačnými směry, pak se uvažuje úhel mezi nimi rozšířený: (180 stupňů). Skalární součin je také záporný, protože

I obrácená tvrzení jsou pravdivá:

1) Jestliže , pak úhel mezi těmito vektory je ostrý. Alternativně jsou vektory ko-směrové.

2) Jestliže , pak úhel mezi těmito vektory je tupý. Alternativně jsou vektory v opačných směrech.

Ale třetí případ je obzvláště zajímavý:

3) Pokud roh mezi vektory rovný: (90 stupňů), tedy skalární součin je nula: . Platí to i obráceně: if , then . Prohlášení lze kompaktně formulovat takto: Skalární součin dvou vektorů je nulový právě tehdy, když jsou vektory ortogonální. Krátký matematický zápis:

! Poznámka : Zopakujme základy matematické logiky: Ikona oboustranného logického důsledku se obvykle čte "když a jen tehdy", "když a jen když". Jak vidíte, šipky směřují oběma směry - "z toho vyplývá toto a naopak - z toho vyplývá toto." Jaký je mimochodem rozdíl od ikony jednosměrného sledování? Ikona uvádí jen to, že, že „z toho vyplývá toto“, a není pravdou, že opak je pravdou. Například: , ale ne každé zvíře je panter, takže v tomto případě nemůžete použít ikonu. Zároveň místo ikony Umět použijte jednostrannou ikonu. Například při řešení problému jsme zjistili, že jsme dospěli k závěru, že vektory jsou ortogonální: - takový záznam bude správný a ještě vhodnější než .

Třetí případ má velký praktický význam, protože vám umožňuje zkontrolovat, zda jsou vektory ortogonální nebo ne. Tento problém vyřešíme ve druhé části lekce.

Vlastnosti bodového produktu

Vraťme se k situaci, kdy dva vektory spolurežírovaný. V tomto případě je úhel mezi nimi nula, a vzorec skalárního součinu má tvar: .

Co se stane, když se vektor vynásobí sám sebou? Je jasné, že vektor je zarovnán sám se sebou, takže použijeme výše uvedený zjednodušený vzorec:

Číslo se volá skalární čtverec vektor a jsou označeny jako .

Tím pádem, skalární čtverec vektoru se rovná druhé mocnině délky daného vektoru:

Z této rovnosti můžeme získat vzorec pro výpočet délky vektoru:

Zatím se to zdá nejasné, ale cíle lekce dají vše na své místo. K vyřešení problémů, které také potřebujeme vlastnosti bodového produktu.

Pro libovolné vektory a libovolné číslo platí následující vlastnosti:

1) – komutativní popř komutativní skalární zákon o součinu.

2) – distribuce popř distribuční skalární zákon o součinu. Jednoduše, můžete otevřít závorky.

3) – asociativní popř asociativní skalární zákon o součinu. Konstantu lze odvodit ze skalárního součinu.

Často jsou všelijaké vlastnosti (které je také potřeba prokázat!) studenty vnímány jako nepotřebné svinstvo, které je potřeba si jen zapamatovat a bezpečně zapomenout ihned po zkoušce. Zdálo by se, že co je zde důležité, každý už od první třídy ví, že přeskupením faktorů se produkt nemění: . Musím vás varovat, že ve vyšší matematice je snadné s takovým přístupem něco pokazit. Takže například komutativní vlastnost není pravdivá pro algebraické matice. To také neplatí pro vektorový součin vektorů. Proto je přinejmenším lepší proniknout do jakýchkoli vlastností, na které narazíte ve vyšším kurzu matematiky, abyste pochopili, co můžete a co nemůžete.

Příklad 3

.

Řešení: Nejprve si ujasněme situaci s vektorem. Co to vůbec je? Součet vektorů je dobře definovaný vektor, který je označen . Geometrický výklad akcí s vektory lze nalézt v článku Vektory pro figuríny. Stejná petržel s vektorem je součtem vektorů a .

Takže podle podmínky je nutné najít skalární součin. Teoreticky musíte použít pracovní vzorec , ale problém je, že neznáme délky vektorů a úhel mezi nimi. Ale podmínka dává podobné parametry pro vektory, takže půjdeme jinou cestou:

(1) Nahraďte výrazy vektorů.

(2) Závorky otevíráme podle pravidla pro násobení mnohočlenů, vulgární jazykolam najdete v článku Komplexní čísla nebo Integrace frakčně-racionální funkce. Nebudu se opakovat =) Mimochodem, distribuční vlastnost skalárního součinu nám umožňuje otevřít závorky. máme právo.

(3) V prvním a posledním členu kompaktně zapíšeme skalární čtverce vektorů: . Ve druhém členu použijeme komutabilitu skalárního součinu: .

(4) Uvádíme podobné termíny: .

(5) V prvním členu používáme vzorec skalárního čtverce, který byl zmíněn nedávno. V posledním termínu tedy funguje totéž: . Druhý člen rozšiřujeme podle standardního vzorce .

(6) Nahraďte tyto podmínky a OPATRNĚ proveďte konečné výpočty.

Odpovědět:

Záporná hodnota skalárního součinu vyjadřuje fakt, že úhel mezi vektory je tupý.

Problém je typický, zde je příklad, jak jej vyřešit sami:

Příklad 4

Najděte skalární součin vektorů a pokud je znám .

Nyní další společný úkol, jen pro nový vzorec pro délku vektoru. Zde se bude zápis trochu překrývat, takže jej pro přehlednost přepíšu jiným písmenem:

Příklad 5

Najděte délku vektoru if .

Řešení bude následující:

(1) Dodáme výraz pro vektor .

(2) Použijeme délkový vzorec: a celý výraz ve funguje jako vektor „ve“.

(3) Pro druhou mocninu součtu použijeme školní vzorec. Všimněte si, jak to tady zvláštním způsobem funguje: – ve skutečnosti je to druhá mocnina rozdílu a ve skutečnosti to tak je. Ti, kteří si přejí, mohou vektory přeskupit: - stane se totéž, až do přeskupení termínů.

(4) To, co následuje, je již známé ze dvou předchozích problémů.

Odpovědět:

Protože mluvíme o délce, nezapomeňte uvést rozměr - „jednotky“.

Příklad 6

Najděte délku vektoru if .

Toto je příklad, který můžete vyřešit sami. Úplné řešení a odpověď na konci lekce.

Pokračujeme ve vymačkávání užitečných věcí z bodového produktu. Podívejme se znovu na náš vzorec . Pomocí pravidla proporce resetujeme délky vektorů na jmenovatele levé strany:

Vyměníme díly:

Jaký je význam tohoto vzorce? Pokud jsou známy délky dvou vektorů a jejich skalární součin, lze vypočítat kosinus úhlu mezi těmito vektory a následně i úhel samotný.

Je bodový součin číslo? Číslo. Jsou délky vektorů čísla? Čísla. To znamená, že zlomek je také číslo. A pokud je kosinus úhlu znám: , pak pomocí inverzní funkce je snadné najít samotný úhel: .

Příklad 7

Najděte úhel mezi vektory a pokud je známo, že .

Řešení: Použijeme vzorec:

V konečné fázi výpočtů byla použita technická technika - odstranění iracionality ve jmenovateli. Abych odstranil iracionalitu, vynásobil jsem čitatele a jmenovatele .

Takže když , Že:

Hodnoty inverzních goniometrických funkcí lze nalézt pomocí trigonometrická tabulka. I když se to stává zřídka. V úlohách analytické geometrie mnohem častěji nějaký nemotorný medvěd jako , a hodnotu úhlu je třeba zjistit přibližně pomocí kalkulačky. Vlastně takový obrázek uvidíme víckrát.

Odpovědět:

Opět nezapomeňte uvést rozměry – radiány a stupně. Osobně, abych zjevně „vyřešil všechny otázky“, dávám přednost označení obou (pokud podmínka samozřejmě nevyžaduje uvedení odpovědi pouze v radiánech nebo pouze ve stupních).

Nyní se můžete samostatně vypořádat se složitějším úkolem:

Příklad 7*

Jsou dány délky vektorů a úhel mezi nimi. Najděte úhel mezi vektory , .

Úkol není ani tak obtížný, jako spíše vícestupňový.
Podívejme se na algoritmus řešení:

1) Podle podmínky musíte najít úhel mezi vektory a , takže musíte použít vzorec .

2) Najděte skalární součin (viz příklady č. 3, 4).

3) Najděte délku vektoru a délku vektoru (viz příklady č. 5, 6).

4) Konec řešení se shoduje s příkladem č. 7 - známe číslo , což znamená, že je snadné najít samotný úhel:

Krátké řešení a odpověď na konci lekce.

Druhá část lekce je věnována stejnému skalárnímu součinu. Souřadnice. Bude to ještě jednodušší než v prvním díle.

Bodový součin vektorů,
dáno souřadnicemi na ortonormálním základě

Odpovědět:

Netřeba dodávat, že práce se souřadnicemi je mnohem příjemnější.

Příklad 14

Najděte skalární součin vektorů a if

Toto je příklad, který můžete vyřešit sami. Zde můžete využít asociativitu operace, tedy nepočítat , ale rovnou vzít trojku mimo skalární součin a vynásobit jím jako poslední. Řešení a odpověď jsou na konci lekce.

Na konci sekce provokativní příklad výpočtu délky vektoru:

Příklad 15

Najděte délky vektorů , Pokud

Řešení: Metoda z předchozí části se opět nabízí: ale existuje i jiný způsob:

Pojďme najít vektor:

A jeho délka podle triviálního vzorce :

Bodový produkt zde není vůbec relevantní!

Není také užitečné při výpočtu délky vektoru:
Stop. Neměli bychom využít zřejmou vlastnost délky vektoru? Co můžete říci o délce vektoru? Tento vektor je 5krát delší než vektor. Směr je opačný, ale to nevadí, protože se bavíme o délce. Je zřejmé, že délka vektoru je rovna součinu modul počet na délku vektoru:
– znaménko modulu „sežere“ možné mínus čísla.

Tím pádem:

Odpovědět:

Vzorec pro kosinus úhlu mezi vektory, které jsou určeny souřadnicemi

Nyní máme kompletní informace pro vyjádření dříve odvozeného vzorce pro kosinus úhlu mezi vektory prostřednictvím souřadnic vektorů:

Kosinus úhlu mezi rovinnými vektory a , specifikované na ortonormálním základě, vyjádřeno vzorcem:
.

Kosinus úhlu mezi prostorovými vektory, specifikované na ortonormálním základě, vyjádřeno vzorcem:

Příklad 16

Jsou dány tři vrcholy trojúhelníku. Najít (vrcholový úhel).

Řešení: Podle podmínek není výkres vyžadován, ale přesto:

Požadovaný úhel je označen zeleným obloukem. Ihned si vzpomeňme na školní označení úhlu: – zvláštní pozornost na průměrný písmeno - to je vrchol úhlu, který potřebujeme. Pro stručnost můžete také napsat jednoduše .

Z výkresu je zcela zřejmé, že úhel trojúhelníku se shoduje s úhlem mezi vektory a jinými slovy: .

Je vhodné naučit se provádět analýzu mentálně.

Pojďme najít vektory:

Vypočítejme skalární součin:

A délky vektorů:

Kosinus úhlu:

Toto je přesně pořadí plnění úkolu, které doporučuji pro figuríny. Pokročilejší čtenáři mohou výpočty napsat „na jeden řádek“:

Zde je příklad „špatné“ hodnoty kosinu. Výsledná hodnota není konečná, takže nemá smysl zbavovat se iracionality ve jmenovateli.

Pojďme najít samotný úhel:

Pokud se podíváte na kresbu, výsledek je docela věrohodný. Pro kontrolu lze úhel také změřit pomocí úhloměru. Nepoškoďte kryt monitoru =)

Odpovědět:

V odpovědi na to nezapomínáme zeptal se na úhel trojúhelníku(a ne o úhlu mezi vektory), nezapomeňte uvést přesnou odpověď: a přibližnou hodnotu úhlu: , nalezený pomocí kalkulačky.

Ti, kteří si tento proces užili, mohou vypočítat úhly a ověřit platnost kanonické rovnosti

Příklad 17

Trojúhelník je definován v prostoru souřadnicemi jeho vrcholů. Najděte úhel mezi stranami a

Toto je příklad, který můžete vyřešit sami. Úplné řešení a odpověď na konci lekce

Krátká závěrečná část bude věnována projekcím, které také zahrnují skalární součin:

Projekce vektoru na vektor. Promítání vektoru na souřadnicové osy.
Směrové kosiny vektoru

Zvažte vektory a:

Promítněme vektor na vektor, k tomu vynecháme začátek a konec vektoru kolmice na vektor (zelené tečkované čáry). Představte si, že paprsky světla dopadají kolmo na vektor. Potom bude segment (červená čára) „stínem“ vektoru. V tomto případě je projekce vektoru na vektor DÉLKA segmentu. Tzn., že PROJEKCE JE ČÍSLO.

Toto ČÍSLO je označeno následovně: , „velký vektor“ označuje vektor KTERÝ projekt, "malý dolní index vektor" označuje vektor NA která se promítá.

Samotný záznam zní takto: „projekce vektoru „a“ na vektor „be“.

Co se stane, když je vektor „být“ „příliš krátký“? Nakreslíme přímku obsahující vektor „být“. A vektor „a“ se již promítne do směru vektoru "být", jednoduše - na přímku obsahující vektor „be“. Totéž se stane, pokud bude vektor „a“ odložen ve třicátém království – bude se stále snadno promítat na přímku obsahující vektor „be“.

Pokud úhel mezi vektory pikantní(jako na obrázku), tedy

Pokud vektory ortogonální, pak (projekce je bod, jehož rozměry jsou považovány za nulové).

Pokud úhel mezi vektory otupit(na obrázku mentálně přeuspořádejte vektorovou šipku), pak (stejně dlouhá, ale se znaménkem mínus).

Nakreslete tyto vektory z jednoho bodu:

Je zřejmé, že když se vektor pohybuje, jeho projekce se nemění

Definice 1

Skalární součin vektorů je číslo rovné součinu dyn těchto vektorů a kosinu úhlu mezi nimi.

Zápis pro součin vektorů a → a b → má tvar a → , b → . Převedeme to do vzorce:

a → , b → = a → · b → · cos a → , b → ^ . a → a b → označují délky vektorů, a → , b → ^ - označení úhlu mezi danými vektory. Pokud je alespoň jeden vektor nulový, to znamená, že má hodnotu 0, bude výsledek roven nule, a → , b → = 0

Když vynásobíme vektor sám o sobě, dostaneme druhou mocninu jeho délky:

a → , b → = a → b → cos a → , a → ^ = a → 2 cos 0 = a → 2

Definice 2

Skalární násobení vektoru samo o sobě se nazývá skalární čtverec.

Vypočteno podle vzorce:

a → , b → = a → · b → · cos a → , b → ^ .

Zápis a → , b → = a → · b → · cos a → , b → ^ = a → · n p a → b → = b → · n p b → a → ukazuje, že n p b → a → je numerická projekce a → na b → , n p a → a → - projekce b → na a →, resp.

Zformulujme definici součinu pro dva vektory:

Skalární součin dvou vektorů a → by b → se nazývá součin délky vektoru a → promítáním b → směrem a → nebo součin délky b → promítáním a →, resp.

Bodový součin v souřadnicích

Skalární součin lze vypočítat pomocí souřadnic vektorů v dané rovině nebo v prostoru.

Skalární součin dvou vektorů v rovině, v trojrozměrném prostoru, se nazývá součet souřadnic daných vektorů a → a b →.

Při výpočtu skalárního součinu daných vektorů a → = (a x , a y) , b → = (b x , b y) na rovině v kartézském systému použijte:

a → , b → = a x b x + a y b y ,

pro trojrozměrný prostor platí výraz:

a → , b → = a x · b x + a y · b y + a z · b z .

Ve skutečnosti se jedná o třetí definici skalárního součinu.

Pojďme to dokázat.

Důkaz 1

Abychom to dokázali, použijeme a → , b → = a → · b → · cos a → , b → ^ = a x · b x + a y · b y pro vektory a → = (a x , a y) , b → = (b x , b y) na kartézském systému.

Vektory by měly být ponechány stranou

O A → = a → = a x , a y a O B → = b → = b x , b y .

Pak bude délka vektoru A B → rovna A B → = O B → - O A → = b → - a → = (b x - a x , b y - a y) .

Uvažujme trojúhelník O A B .

A B 2 = O A 2 + O B 2 - 2 · O A · O B · cos (∠ A O B) je správné na základě kosinové věty.

Podle podmínky je jasné, že O A = a → , O B = b → , A B = b → - a → , ∠ A O B = a → , b → ^ , což znamená, že vzorec pro zjištění úhlu mezi vektory napíšeme jinak.

b → - a → 2 = a → 2 + b → 2 - 2 · a → · b → · cos (a → , b → ^) .

Z první definice pak vyplývá, že b → - a → 2 = a → 2 + b → 2 - 2 · (a → , b →) , což znamená (a → , b →) = 1 2 · (a → 2 + b → 2 - b → - a → 2) .

Použitím vzorce pro výpočet délky vektorů dostaneme:
a → , b → = 1 2 · ((a 2 x + a y 2) 2 + (b 2 x + b y 2) 2 - ((b x - a x) 2 + (b y - a y) 2) 2) = = 1 2 (a 2 x + a 2 y + b 2 x + b 2 y - (b x - a x) 2 - (b y - a y) 2) = = a x b x + a y b y

Dokažme rovnost:

(a → , b →) = a → b → cos (a → , b → ^) = = a x b x + a y b y + a z b z

– respektive pro vektory trojrozměrného prostoru.

Skalární součin vektorů se souřadnicemi říká, že skalární čtverec vektoru je roven součtu druhých mocnin jeho souřadnic v prostoru a v rovině. a → = (ax, ay, az), b → = (b x, b y, b z) a (a → , a →) = a x 2 + a y 2 .

Bodový produkt a jeho vlastnosti

Existují vlastnosti bodového součinu, které platí pro a → , b → a c → :

1. komutativnost (a → , b →) = (b → , a →) ;
2. distributivita (a → + b → , c →) = (a → , c →) + (b → , c →) , (a → + b → , c →) = (a → , b →) + (a → , c →) ;
3. kombinační vlastnost (λ · a → , b →) = λ · (a → , b →), (a → , λ · b →) = λ · (a → , b →), λ - libovolné číslo;
4. skalární čtverec je vždy větší než nula (a → , a →) ≥ 0, kde (a → , a →) = 0 v případě, že a → nula.

Vlastnosti jsou vysvětlitelné díky definici skalárního součinu na rovině a vlastnostem sčítání a násobení reálných čísel.

Dokažte komutativní vlastnost (a → , b →) = (b → , a →) . Z definice máme, že (a → , b →) = a y · b y + a y · b y a (b → , a →) = b x · a x + b y · a y .

Vlastností komutativnosti platí, že rovnosti a x · b x = b x · a x a a y · b y = b y · a y jsou pravdivé, což znamená a x · b x + a y · b y = b x · a x + b y · a y .

Z toho vyplývá, že (a → , b →) = (b → , a →) . Q.E.D.

Distributivita platí pro všechna čísla:

(a (1) → + a (2) → + ... + a (n) → , b →) = (a (1) → , b →) + (a (2) → , b →) + . . . + (a (n) → , b →)

a (a → , b (1) → + b (2) → + .. + b (n) →) = (a → , b (1) →) + (a → , b (2) →) +. . . + (a → , b → (n)),

proto máme

(a (1) → + a (2) → + ... + a (n) → , b (1) → + b (2) → + ... + b (m) →) = = (a ( 1) → , b (1) →) + (a (1) → , b (2) →) + . . . + (a (1) → , b (m) →) + + (a (2) → , b (1) →) + (a (2) → , b (2) →) + . . . + (a (2) → , b (m) →) + . . . + + (a (n) → , b (1) →) + (a (n) → , b (2) →) + . . . + (a (n) → , b (m) →)

Dot produkt s příklady a řešení

Jakýkoli problém tohoto druhu se řeší pomocí vlastností a vzorců vztahujících se ke skalárnímu součinu:

1. (a → , b →) = a → · b → · cos (a → , b → ^) ;
2. (a → , b →) = a → · n p a → b → = b → · n p b → a → ;
3. (a → , b →) = a x · b x + a y · b y nebo (a → , b →) = a x · b x + a y · b y + a z · b z;
4. (a → , a →) = a → 2 .

Podívejme se na několik příkladů řešení.

Příklad 2

Délka a → je 3, délka b → je 7. Najděte součin tečky, pokud má úhel 60 stupňů.

Řešení

Podle podmínky máme všechna data, takže je vypočítáme pomocí vzorce:

(a → , b →) = a → b → cos (a → , b → ^) = 3 7 cos 60 ° = 3 7 1 2 = 21 2

Odpověď: (a → , b →) = 21 2 .

Příklad 3

Dané vektory a → = (1 , - 1 , 2 - 3) , b → = (0 , 2 , 2 + 3) . Co je to skalární součin?

Řešení

Tento příklad uvažuje vzorec pro výpočet souřadnic, protože jsou uvedeny v příkazu k problému:

(a → , b →) = a x · b x + a y · b y + a z · b z = = 1 · 0 + (- 1) · 2 + (2 + 3) · (2 ​​​​+ 3) = = 0 - 2 + (2-9) = -9

Odpověď: (a → , b →) = - 9

Příklad 4

Najděte skalární součin A B → a A C →. Na souřadnicové rovině jsou dány body A (1, - 3), B (5, 4), C (1, 1).

Řešení

Nejprve se vypočítají souřadnice vektorů, protože podle podmínky jsou souřadnice bodů dány:

A B → = (5 - 1, 4 - (- 3)) = (4, 7) A C → = (1 - 1, 1 - (- 3)) = (0, 4)

Dosazením do vzorce pomocí souřadnic dostaneme:

(A B →, AC →) = 40 + 74 = 0 + 28 = 28.

Odpověď: (A B → , A C →) = 28 .

Příklad 5

Dané vektory a → = 7 · m → + 3 · n → a b → = 5 · m → + 8 · n → , najděte jejich součin. m → se rovná 3 an → rovná se 2 jednotkám, jsou kolmé.

Řešení

(a → , b →) = (7 m → + 3 n → , 5 m → + 8 n →) . Aplikováním vlastnosti distributivity dostaneme:

(7 m → + 3 n →, 5 m → + 8 n →) = = (7 m →, 5 m →) + (7 m →, 8 n →) + (3 n → , 5 m →) + ( 3 n → , 8 n →)

Odebereme koeficient ze znaménka součinu a dostaneme:

(7 m → , 5 m →) + (7 m → , 8 n →) + (3 n → , 5 m →) + (3 n → , 8 n →) = = 7 · 5 · (m → , m →) + 7 · 8 · (m → , n →) + 3 · 5 · (n → , m →) + 3 · 8 · (n → , n →) = = 35 · (m → , m →) + 56 · (m → , n →) + 15 · (n → , m →) + 24 · (n → , n →)

Vlastností komutativnosti transformujeme:

35 · (m → , m →) + 56 · (m → , n →) + 15 · (n → , m →) + 24 · (n → , n →) = = 35 · (m → , m →) + 56 · (m → , n →) + 15 · (m → , n →) + 24 · (n → , n →) = = 35 · (m → , m →) + 71 · (m → , n → ) + 24 · (n → , n →)

V důsledku toho dostaneme:

(a → , b →) = 35 · (m → , m →) + 71 · (m → , n →) + 24 · (n → , n →).

Nyní použijeme vzorec pro skalární součin s úhlem určeným podmínkou:

(a → , b →) = 35 · (m → , m →) + 71 · (m → , n →) + 24 · (n → , n →) = = 35 · m → 2 + 71 · m → · n → · cos (m → , n → ^) + 24 · n → 2 = 35 · 3 2 + 71 · 3 · 2 · cos π 2 + 24 · 2 2 = 411 .

Odpověď: (a → , b →) = 411

Pokud existuje numerická projekce.

Příklad 6

Najděte skalární součin a → a b →. Vektor a → má souřadnice a → = (9, 3, - 3), projekce b → se souřadnicemi (- 3, - 1, 1).

Řešení

Podmínkou jsou vektory a → a projekce b → opačně, protože a → = - 1 3 · n p a → b → → , což znamená, že projekce b → odpovídá délce n p a → b → → , a s „ -" podepsat:

n p a → b → → = - n p a → b → → = - (- 3) 2 + (- 1) 2 + 1 2 = - 11 ,

Dosazením do vzorce dostaneme výraz:

(a → , b →) = a → · n p a → b → → = 9 2 + 3 2 + (- 3) 2 · (- 11) = - 33 .

Odpověď: (a → , b →) = - 33 .

Problémy se známým skalárním součinem, kdy je potřeba najít délku vektoru nebo numerické projekce.

Příklad 7

Jakou hodnotu má mít λ pro daný skalární součin a → = (1, 0, λ + 1) a b → = (λ, 1, λ) se bude rovnat -1.

Řešení

Ze vzorce je zřejmé, že je nutné najít součet součinů souřadnic:

(a →, b →) = 1 λ + 0 1 + (λ + 1) λ = λ 2 + 2 λ.

Máme-li (a → , b →) = - 1 .

Abychom našli λ, vypočítáme rovnici:

λ 2 + 2 · λ = - 1, tedy λ = - 1.

Odpověď: λ = - 1.

Fyzikální význam skalárního součinu

Mechanika zvažuje aplikaci bodového součinu.

Když A pracuje konstantní silou F → pohybující se těleso z bodu M do N, můžete najít součin délek vektorů F → a M N → s kosinusem úhlu mezi nimi, což znamená, že práce je stejná na součin vektorů síly a výchylky:

A = (F → , M N →) .

Příklad 8

Pohyb hmotného bodu o 3 metry pod vlivem síly rovnající se 5 Ntonům je veden pod úhlem 45 stupňů vzhledem k ose. Najdi.

Řešení

Protože práce je součin vektoru síly a posunutí, znamená to, že na základě podmínky F → = 5, S → = 3, (F →, S → ^) = 45 ° dostaneme A = (F →, S →) = F → · S → · cos (F → , S → ^) = 5 · 3 · cos (45 °) = 15 2 2 .

Odpověď: A = 15 2 2 .

Příklad 9

Hmotný bod pohybující se z M (2, - 1, - 3) do N (5, 3 λ - 2, 4) působením síly F → = (3, 1, 2) vykonal práci rovnou 13 J. Vypočítejte délka pohybu.

Řešení

Pro dané vektorové souřadnice M N → máme M N → = (5 - 2, 3 λ - 2 - (- 1) , 4 - (- 3)) = (3, 3 λ - 1, 7) .

Pomocí vzorce pro hledání práce s vektory F → = (3, 1, 2) a M N → = (3, 3 λ - 1, 7) získáme A = (F ⇒, M N →) = 3 3 + 1 ( 3 λ - 1) + 2 7 = 22 + 3 λ.

Podle podmínky je dáno, že A = 13 J, což znamená 22 + 3 λ = 13. To znamená λ = - 3, což znamená M N → = (3, 3 λ - 1, 7) = (3, - 10, 7).

Chcete-li zjistit délku pohybu M N →, použijte vzorec a dosaďte hodnoty:

MN -> = 32 + (- 10)2 + 72 = 158.

Odpověď: 158.

Pokud si všimnete chyby v textu, zvýrazněte ji a stiskněte Ctrl+Enter

Budou zde také problémy, které budete muset vyřešit sami, na které můžete vidět odpovědi.

Pokud jsou v problému jak délky vektorů, tak úhel mezi nimi prezentovány „na stříbrném podnose“, pak podmínka problému a jeho řešení vypadá takto:

Příklad 1 Jsou uvedeny vektory. Najděte skalární součin vektorů, pokud jsou jejich délky a úhel mezi nimi reprezentovány následujícími hodnotami:

Platí i jiná definice, zcela ekvivalentní definici 1.

Definice 2. Skalární součin vektorů je číslo (skalární) rovné součinu délky jednoho z těchto vektorů a průmětu jiného vektoru na osu určenou prvním z těchto vektorů. Vzorec podle definice 2:

Úlohu vyřešíme pomocí tohoto vzorce po dalším důležitém teoretickém bodu.

Definice skalárního součinu vektorů z hlediska souřadnic

Stejné číslo lze získat, pokud vektorům, které se násobí, budou uvedeny jejich souřadnice.

Definice 3. Bodový součin vektorů je číslo rovné součtu párových součinů jejich odpovídajících souřadnic.

Na povrchu

Jsou-li dva vektory a na rovině definovány svými dvěma Kartézské pravoúhlé souřadnice

pak se skalární součin těchto vektorů rovná součtu párových součinů jejich odpovídajících souřadnic:

.

Příklad 2 Najděte číselnou hodnotu průmětu vektoru na osu rovnoběžnou s vektorem.

Řešení. Skalární součin vektorů najdeme sečtením párových součinů jejich souřadnic:

Nyní musíme výsledný skalární součin přirovnat k součinu délky vektoru a průmětu vektoru na osu rovnoběžnou s vektorem (v souladu se vzorcem).

Délku vektoru zjistíme jako druhou odmocninu součtu druhých mocnin jeho souřadnic:

.

Vytvoříme rovnici a vyřešíme ji:

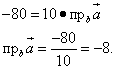
Odpovědět. Požadovaná číselná hodnota je mínus 8.

Ve vesmíru

Jsou-li dva vektory a v prostoru definovány svými třemi kartézskými pravoúhlými souřadnicemi

,

pak se skalární součin těchto vektorů také rovná součtu párových součinů jejich odpovídajících souřadnic, pouze už existují tři souřadnice:

.

Úkolem najít skalární součin pomocí uvažované metody je po analýze vlastností skalárního součinu. Protože v problému budete muset určit, jaký úhel tvoří vynásobené vektory.

Vlastnosti skalárního součinu vektorů

Algebraické vlastnosti

1. (komutativní vlastnost: obrácení míst vynásobených vektorů nezmění hodnotu jejich skalárního součinu).

2. (asociativní vlastnost s ohledem na číselný faktor: skalární součin vektoru vynásobený určitým faktorem a jiného vektoru je roven skalárnímu součinu těchto vektorů vynásobeného stejným faktorem).

3. (distributivní vlastnost vzhledem k součtu vektorů: skalární součin součtu dvou vektorů třetím vektorem je roven součtu skalárních součinů prvního vektoru třetím vektorem a druhého vektoru třetím vektorem).

4. (skalární čtverec vektoru větší než nula), if je nenulový vektor a , if je nulový vektor.

Geometrické vlastnosti

V definicích zkoumané operace jsme se již dotkli pojmu úhel mezi dvěma vektory. Je čas si tento pojem ujasnit.

Na obrázku výše můžete vidět dva vektory, které jsou přivedeny ke společnému počátku. A první věc, kterou musíte věnovat pozornost, je, že mezi těmito vektory jsou dva úhly - φ 1 A φ 2 . Který z těchto úhlů se objevuje v definicích a vlastnostech skalárního součinu vektorů? Součet uvažovaných úhlů je 2 π a proto jsou kosiny těchto úhlů stejné. Definice bodového součinu zahrnuje pouze kosinus úhlu, nikoli hodnotu jeho vyjádření. Ale vlastnosti berou v úvahu pouze jeden úhel. A to je jeden ze dvou úhlů, který nepřesahuje π , tedy 180 stupňů. Na obrázku je tento úhel označen jako φ 1 .

1. Jsou volány dva vektory ortogonální A úhel mezi těmito vektory je rovný (90 stupňů resp π /2 ), pokud skalární součin těchto vektorů je nula :

.

Ortogonalita ve vektorové algebře je kolmost dvou vektorů.

2. Dva nenulové vektory tvoří ostrý roh (od 0 do 90 stupňů, nebo, což je stejné - méně π dot product je pozitivní .

3. Dva nenulové vektory tvoří tupý úhel (od 90 do 180 stupňů, nebo, co je stejné - více π /2) tehdy a jen tehdy, když oni dot product je negativní .

Příklad 3 Souřadnice jsou dány vektory:

.

Vypočítejte skalární součiny všech dvojic daných vektorů. Jaký úhel (akutní, pravý, tupý) tvoří tyto dvojice vektorů?

Řešení. Budeme počítat sečtením součinů odpovídajících souřadnic.

Dostali jsme záporné číslo, takže vektory svírají tupý úhel.

Dostali jsme kladné číslo, takže vektory svírají ostrý úhel.

Dostali jsme nulu, takže vektory svírají pravý úhel.

Dostali jsme kladné číslo, takže vektory svírají ostrý úhel.

.

Dostali jsme kladné číslo, takže vektory svírají ostrý úhel.

Pro autotest můžete použít online kalkulačka Bodový součin vektorů a kosinus úhlu mezi nimi .

Příklad 4. Vzhledem k délkám dvou vektorů a úhlu mezi nimi:

.

Určete, při jaké hodnotě čísla jsou vektory a ortogonální (kolmé).

Řešení. Vynásobme vektory pomocí pravidla pro násobení polynomů:

Nyní spočítáme každý termín:

.

Vytvořme rovnici (součin se rovná nule), přidáme podobné členy a rovnici vyřešíme:

Odpověď: dostali jsme hodnotu λ = 1,8, při kterém jsou vektory ortogonální.

Příklad 5. Dokažte, že vektor ortogonální (kolmý) k vektoru

Řešení. Abychom ověřili ortogonalitu, vynásobíme vektory a jako polynomy, místo toho dosadíme výraz uvedený v příkazu k problému:

.

Chcete-li to provést, musíte vynásobit každý člen (člen) prvního polynomu každým členem druhého a sečíst výsledné produkty:

.

Ve výsledném výsledku se zlomek sníží o. Získá se následující výsledek:

Závěr: v důsledku násobení jsme dostali nulu, proto je ortogonalita (kolmost) vektorů prokázána.

Vyřešte problém sami a pak se podívejte na řešení

Příklad 6. Délky vektorů a jsou dány a úhel mezi těmito vektory je π /4 . Určete v jaké hodnotě μ vektory a jsou vzájemně kolmé.

Pro autotest můžete použít online kalkulačka Bodový součin vektorů a kosinus úhlu mezi nimi .

Maticová reprezentace bodového součinu vektorů a součinu n-rozměrných vektorů

Někdy je pro přehlednost výhodné znázornit dva vynásobené vektory ve formě matic. Pak je první vektor reprezentován jako řádková matice a druhý - jako sloupcová matice:

Pak bude skalární součin vektorů součin těchto matric :

Výsledek je stejný jako výsledek získaný metodou, kterou jsme již uvažovali. Dostali jsme jedno jediné číslo a součin řádkové matice a sloupcové matice je také jedno jediné číslo.

Je vhodné reprezentovat součin abstraktních n-rozměrných vektorů v maticové formě. Tedy součin dvou čtyřrozměrných vektorů bude součin řádkové matice se čtyřmi prvky sloupcovou maticí rovněž se čtyřmi prvky, součin dvou pětirozměrných vektorů bude součin řádkové matice s pěti prvky o sloupcová matice také s pěti prvky a tak dále.

Příklad 7. Najděte skalární součiny dvojic vektorů

,

pomocí maticové reprezentace.

Řešení. První dvojice vektorů. První vektor reprezentujeme jako řádkovou matici a druhý jako sloupcovou matici. Skalární součin těchto vektorů najdeme jako součin řádkové matice a sloupcové matice:

Podobně reprezentujeme druhý pár a zjistíme:

Jak vidíte, výsledky byly stejné jako u stejných párů z příkladu 2.

Úhel mezi dvěma vektory

Odvození vzorce pro kosinus úhlu mezi dvěma vektory je velmi krásné a výstižné.

K vyjádření bodového součinu vektorů

(1)

v souřadnicovém tvaru nejprve najdeme skalární součin jednotkových vektorů. Skalární součin vektoru se sebou samým podle definice:

To, co je napsáno ve vzorci výše, znamená: skalární součin vektoru sám se sebou se rovná druhé mocnině jeho délky. Kosinus nuly je roven jedné, takže druhá mocnina každé jednotky bude rovna jedné:

Protože vektory

jsou párově kolmé, pak se párové součiny jednotkových vektorů budou rovnat nule:

Nyní provedeme násobení vektorových polynomů:

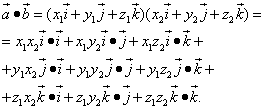
Do pravé strany rovnosti dosadíme hodnoty odpovídajících skalárních součinů jednotkových vektorů:

Získáme vzorec pro kosinus úhlu mezi dvěma vektory:

Příklad 8. Udělují se tři body A(1;1;1), B(2;2;1), C(2;1;2).

Najděte úhel.

Řešení. Zjištění souřadnic vektorů:

,

.

Pomocí vzorce kosinového úhlu dostaneme:

Proto, .

Pro autotest můžete použít online kalkulačka Bodový součin vektorů a kosinus úhlu mezi nimi .

Příklad 9. Jsou dány dva vektory

Najděte součet, rozdíl, délku, bodový součin a úhel mezi nimi.

2. Rozdíl

Přednáška: Vektorové souřadnice; skalární součin vektorů; úhel mezi vektory

Vektorové souřadnice

Takže, jak již bylo zmíněno dříve, vektor je směrovaný segment, který má svůj vlastní začátek a konec. Pokud jsou začátek a konec reprezentovány určitými body, pak mají své vlastní souřadnice v rovině nebo v prostoru.

Pokud má každý bod své souřadnice, pak můžeme získat souřadnice celého vektoru.

Řekněme, že máme vektor, jehož začátek a konec mají následující označení a souřadnice: A(A x ; Ay) a B(B x ; By)

Pro získání souřadnic daného vektoru je nutné odečíst odpovídající souřadnice začátku od souřadnic konce vektoru:

Chcete-li určit souřadnice vektoru v prostoru, použijte následující vzorec:

Bodový součin vektorů

Existují dva způsoby, jak definovat koncept skalárního produktu:

• Geometrická metoda. Podle něj se skalární součin rovná součinu hodnot těchto modulů a kosinu úhlu mezi nimi.

• Algebraický význam. Skalárním součinem dvou vektorů je z hlediska algebry určitá veličina, která se získá jako výsledek součtu součinů odpovídajících vektorů.

Pokud jsou vektory uvedeny v prostoru, měli byste použít podobný vzorec:

Vlastnosti:

• Pokud vynásobíte dva stejné vektory skalárně, jejich skalární součin nebude záporný:

• Pokud se skalární součin dvou identických vektorů rovná nule, pak jsou tyto vektory považovány za nulové:

• Pokud se určitý vektor vynásobí sám sebou, pak se skalární součin bude rovnat druhé mocnině jeho modulu:

• Skalární součin má komunikační vlastnost, to znamená, že skalární součin se nezmění, pokud se vektory přeuspořádají:

• Skalární součin nenulových vektorů se může rovnat nule, pouze pokud jsou vektory na sebe kolmé:

• Pro skalární součin vektorů platí komutativní zákon v případě vynásobení jednoho z vektorů číslem:

• Se skalárním součinem můžete také použít distribuční vlastnost násobení:

Úhel mezi vektory